Distributions in Data Science

Discrete Distributions

These are used when the variable can take on only specific, separate values (usually counts).

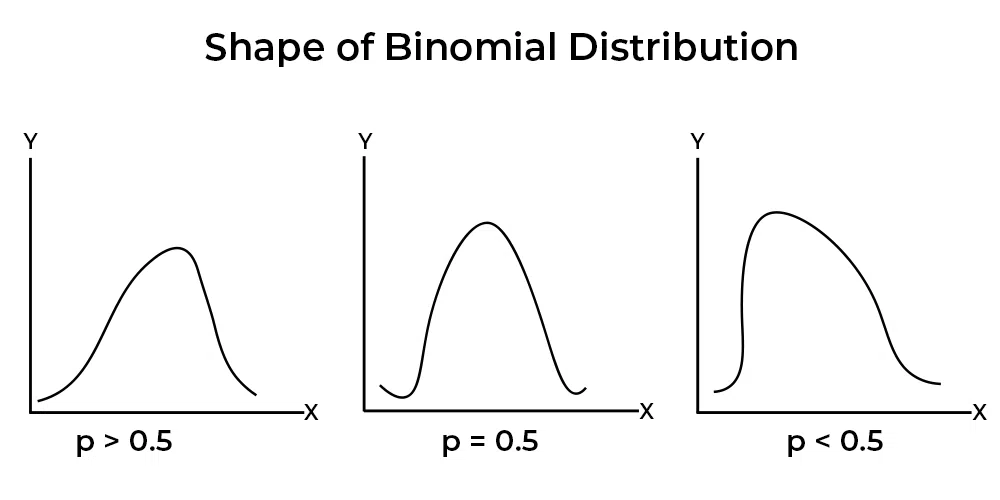
Binomial Distribution

Use: Models the number of successes in a fixed number of independent Bernoulli trials.

Example: Number of defective items in a batch of 100.

Formula for binomial distribution is

$$P(X=x){=}^n{C}_x{q}^{n-x},x=0,1,2,......,n;0<p<1$$

where, $P(X=x)$ represents the probability of getting x successes in n experiments,
${}^n{C}_x$ is the binomial coefficient and is equal to $\frac{n!}{x!(n-x)!}$$p$ is the probability of success in a single experiment.
$q$ is the probability of failure in a single experiment, and $q=1-p$
$n$ is the total number of experiments.

Mean: $\mu =np$
Variance: $\sigma ²=npq$

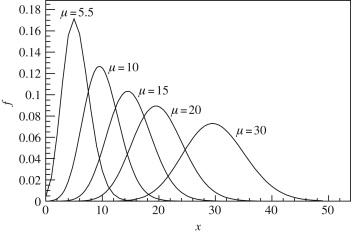
Poisson Distribution

Use: Models the number of events occurring in a fixed interval of time or space.

Example: Number of calls received at a call center in an hour.

Formula:

$$P(X=x)=\frac{{\lambda }^x{e}^{-\lambda }}{x!},x=1,2,3,.....;\lambda >0$$

where,

$P(x)$ represents the probability of a specific number of events occurring. $e$ is the mathematical constant approximately equal to 2.7183. $\lambda$ is the average rate of event occurrences in the given time or space.

Mean and Variance can be calculated as:

$$\mu ={\sigma }^2=\lambda$$

Geometric Distribution

Use: Models the number of trials until the first success.

Example: Number of coin tosses until the first heads.

Negative Binomial Distribution

Use: Models the number of trials needed to achieve a specified number of successes.

Example: Number of customers visited until 5 sales are made.

Hypergeometric Distribution

Use: Models successes in draws without replacement from a finite population.

Example: Number of red balls drawn from a bag without putting them back.

Continuous Distributions

Used when the variable can take any value in an interval (e.g., time, weight, cost).

Normal Distribution (Gaussian)

Use: Most commonly used; describes natural phenomena like measurement errors.

Example: Heights of people, test scores.

Exponential Distribution

Use: Models time between events in a Poisson process.

Example: Time between arrivals at a service point.

Uniform Distribution

Use: All outcomes in an interval are equally likely.

Example: Time taken for a process that can vary uniformly between 2 and 10 minutes.

Log-Normal Distribution

Use: Models variables whose logarithm is normally distributed.

Example: Stock prices, income distribution.

Gamma Distribution

Use: Models waiting times when multiple events are expected.

Example: Time to complete k tasks.

Beta Distribution

Use: Useful in Bayesian statistics and modeling probabilities themselves.

Example: Estimating the probability of success in project completion.

Weibull Distribution

Use: Common in reliability and survival analysis.

Example: Failure times of machines or components.

Other Relevant Distributions

Multinomial Distribution

Extension of the binomial distribution for multi-category outcomes.

Chi-Square Distribution

Used in hypothesis testing and confidence interval estimation for variance.

t-Distribution

Used in small sample statistical inference for means.

F-Distribution

Used in analysis of variance (ANOVA) and regression.